Deep Representation Learning

At GlassRoom, we use deep learning, not to make predictions, but to transform data into more useful representations, a process AI researchers commonly refer to as deep representation learning.

The only comprehensive introduction to the subject we have found online, at the time of writing (early 2018), is the "Representation Learning" chapter of the textbook "Deep Learning," by Ian Goodfellow, Yoshua Bengio and Aaron Courville. However, this textbook is intended for individuals with a serious interest in the subject such as graduate and undergraduate students enrolled in AI courses or software engineers developing AI applications. To the best of our knowledge, there are no introductions to the subject suitable for a broader audience.

We aim to fill the vacuum with this web page.

Below, we will explain in everyday English what deep representation learning is, why and when it is necessary, and how we use it at GlassRoom. We will skip over the mathematical details, so as to not make anybody run in fear, but otherwise our descriptions will be as accurate as possible. We will assume you know very little to start with, but by the end you will be reading about fairly advanced topics, such as zero-shot learning, a seemingly impossible feat in which a computer learns to perform a task without first seeing examples of it.

What Is a Representation?

At a restaurant near our offices, sometimes the soup of the day is chicken tortilla soup. Now, consider this: you understood what the words chicken tortilla soup meant, even though there was no mention of the soup's particular taste, texture, toppings, serving size, appearance, temperature, ingredients, molecular composition, or any other specifics. The 21 letters and spaces making up "chicken tortilla soup" conveyed sufficient information.

Obviously, those 21 characters are not the soup. They are a representation of the abstract concept of a chicken tortilla soup. The representation itself consists only of meaningless symbols like "c" and "h" from the Latin alphabet, organized according to the conventions of written English. The concept is an abstract one because it doesn't contain information specific to concrete examples of the soup -- taste, texture, toppings, etc.

Less obviously, the representation makes sense to us only because it is coherent with the patterns of organization of other representations constructed from the same symbols and conventions. Combinations of the same symbols that are not coherent with the patterns of organization of written English, such as "kldfh werrf jrthsjs" and "ooopd fkqr bnsaod," are meaningless in written English; they don't represent anything.

If you search online for "chicken tortilla soup," you will find descriptions of and recipes for the soup written in English -- what else? Those descriptions and recipes are representations too, made up of the same meaningless symbols from the Latin alphabet, organized into complicated patterns of paragraphs, sentences, phrases, and words according to the conventions of the language.

Every representation in written English, in fact, is defined in terms of other representations constructed from the same set of symbols and conventions, in an infinite regress. The Oxford English Dictionary and Merriam-Webster's Dictionary are marvels of never-ending self-reference. So is every encyclopedia, including the world's largest, Wikipedia. Dictionaries and encyclopedias are constructed like the "Drawing Hands" of M. C. Escher:

We could use a different set of conventions for constructing representations (e.g., the conventions of French, German, or Spanish) or even a different set of symbols (e.g., logograms from Chinese Hànzì, or dots and dashes from Morse Code), but the representation of a chicken tortilla soup must be coherent with the patterns of organization of all other representations constructed from the same symbols and conventions.

The entire edifice of written language, as it were, rests on those patterns of organization. Indeed, those patterns must be coherent with each other for us to understand written language.

This is true not only for all written languages we read with our eyes (or fingertips, in the case of Braille), but also for all other kinds of representations we perceive through our senses. For example, the waves of changing air pressure that reach our ears when someone nearby says "chicken tortilla soup" must be coherent with the patterns of organization of other sounds we hear; otherwise, we wouldn't understand spoken language. Similarly, the many millions of photons that hit our retinas every second we look at a chicken tortilla soup must be coherent with the patterns of organization of the many other millions of photons that reach our eyes after bouncing off other visible objects; otherwise, we wouldn't understand what we see.

It must be true for everything we think too. The neuron activations in our brain that represent the thought "chicken tortilla soup" must be coherent with the patterns of organization of other neuron activations in our brain; otherwise, we wouldn't be able to think of the soup. Hence we should be able to use other symbols instead of neuron activations to represent our thoughts. The notion might seem far-fetched, but in fact, that is precisely what we do with the meaningless symbols of written language: we represent thoughts with them.

Representation Learning

When we say "representation learning," deep or not, we mean machine learning in which the goal is to learn to transform data from its original representation to a new representation that retains information essential to objects that are of interest to us, while discarding other information. The transformation is analogous to the manner in which we transformed neuron activations in our brains, representing a nearby restaurant's chicken tortilla soup, into a new representation consisting of 21 characters in written English. The new representation in written English retains the essential features of a chicken tortilla soup (the object of interest), but discards other information, including details specific to the nearby restaurant's particular version of the soup.

Three examples of representation learning that we will examine are: (1) machine learning software that learns to transform words into representations of their syntactic and semantic relationships with other words; (2) machine learning software that learns to transform digital photos into representations of the kinds of objects they depict; and (3) machine learning software that learns to transform sentences into representations of their meaning. The emphasized words denote the objects of interest in each case. We will examine these examples after we have covered a few key concepts necessary for understanding them.

Representations in a computer consist of sequences of binary digits, or bits, typically organized into floating-point numbers. The choice of bits -- digital ones and zeros -- as symbols for the construction of representations inside computers is not important for our purposes. What is important is that the new representations, each one consisting of a sequence of bits, must be coherent in the sense explained earlier with the patterns of organization of all other bit representations of input data transformed in the same manner.

The entire edifice of the new representation scheme, as it were, rests on the patterns of organization of all possible sequences of bits representing different objects in the new scheme. Indeed, those patterns must be coherent with each other for there to be a representation scheme.

Mathematical Transformation of Statistical Patterns

The patterns of organization of the new representation scheme, like all patterns of organization, are of a statistical nature: they specify how and under which conditions bits can combine with each other to form representations. Thus the transformation from the original representation scheme to the new representation scheme is a mathematical transformation -- possibly a very complicated one, but one which therefore can be implemented as a mechanistic sequence of computational steps that manipulate bits. In other words, the transformation is done by software.

Depending on your mathematical sophistication, you might find it difficult to imagine how such a transformation could ever be implemented as a robotic sequence of steps that manipulate bits. The reason for this difficulty is that the kind of transformation we are discussing here cannot be easily imagined, or even properly understood, without first learning to reason about fairly abstract mathematical and software concepts to which most people are never exposed in their lifetime. However, you don't need to understand the mathematical details to grasp the idea that the transformation of statistical patterns to the new representation scheme is of a mathematical nature and therefore is implemented in machine learning software.

If the machine learning software that learns to perform this kind of transformation is an artificial neural network with many layers of neurons, or deep neural net for short, we call the process of learning to transform the input data in this special way deep representation learning.

How Deep Neural Nets Learn Representations

In order to explain how deep neural nets learn representations, we must first take a brief detour to explain how they learn to make predictions, for reasons that will become obvious shortly.

At present, deep neural nets learn to make predictions via an iterative training process, during which we repeatedly feed sample input data and gradually adjust the behavior of all layers of neurons in the neural net so they jointly learn to transform input data into good predictions. We, the makers of the neural net, decide what those predictions should be and also specify precisely how to measure their goodness to induce learning.

During training, each layer of neurons learns to transform its inputs into a different representation. This representation is itself an input to subsequent layers, which, in turn, learn to transform it into yet other representations. Eventually, we reach the final layer, which learns to transform the last representation into good predictions (however specified). Each layer, in effect, learns to make the next layer's job a little easier:

In the case of a feedforward deep neural net like the one depicted above, the layers tend to get smaller (i.e., contain fewer neurons) the deeper we go into the neural net. During training, this neural net is thus "architecturally biased" to learn to transform input data into progressively smaller representations that retain the information necessary for making good predictions. The deeper we go into this neural net, the smaller the representations get, and the more abstract they become. The final layer learns to transform highly abstract representations of input data into good predictions.

For example, if the initial layer's input contains millions of pixel values representing a digital photo, the final layer's input, i.e., the last representation, might contain a few thousand values which together indicate, say, the likely presence or absence of certain kinds of objects in the photo. If the initial layer's input contains a sequence of bit values representing text, the last representation might contain values which together indicate, say, the likely presence or absence of certain patterns of thought in the text.

In case you are wondering: yes, this is a form of intelligence -- a rudimentary, human-guided, artificial form of perceptual intelligence, but intelligence nonetheless. (What else could it be?)

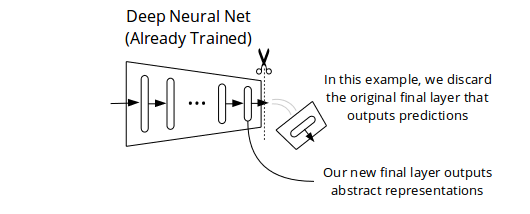
We Discard the Predictions and Keep the Representations

Once a neural net is trained as described above, we can perform surgery on it, so it outputs representations instead of predictions when presented with new input data. For example, let's say we have a feedforward neural net that has already learned to make good predictions (however we specified them during training). We slice off its last layer, as shown below, and voilà! We end up with a slightly shorter neural net, which, when fed input data, outputs an abstract representation of it.

We can use the representations produced by this shorter neural net for a purpose different than the prediction objectives we specified to induce learning in the training phase. For example, we could feed the representations as inputs to a second neural net for a different learning task. The second neural net would benefit from the representational knowledge learned by the first one -- that is, assuming the prediction objectives we specified to train the first neural net induced learning of representations useful for the second one.

If the main or only purpose of training a neural net is to learn useful representations, the discarded prediction objectives are more accurately described as training objectives.

We Engineer the Training Objectives to Learn Useful Representations

This is the essence of deep representation learning. The training objectives we specify to induce learning in the training phase, along with the architecture of a neural net (e.g., number, sizes, types, and arrangement of layers), determine what kinds of representations the neural net learns. Our job is to come up with training objectives and suitable architectures that together induce learning of the kinds of representations we want as a byproduct. The goal is not to make predictions per se, but to learn useful representations of input data.

For historical reasons, many machine learning practitioners would refer to this kind of deep learning as "unsupervised." However, we think the term is a misnomer, because there is nothing unsupervised about engineering training objectives. In fact, a key long-term goal of AI research is to figure out how to engineer training objectives (and suitable architectures) that can learn to represent the world around us.

Probably the best way to explain how we engineer training objectives is with illustrative examples.

Three Illustrative Examples

We will examine three neural net designs from a high-level, non-technical perspective: (1) a neural net that learns to transform written words into representations of their syntactic and semantic relationships with other words; (2) a deep neural net that learns to transform digital photos into representations of the kinds of objects they depict; and (3) a deep neural net that learns to transform sentences into representations of their meaning. The emphasized words, as before, denote the objects of interest in each case.

As you read about each example, put yourself in the shoes of the AI researchers who engineered the training objectives, and ponder how and why those training objectives induce learning of useful representations.

Example #1: Learning Representations of Word Relationships by Predicting Context

Our first example will be the simplest: a neural net model conceived by AI researchers at Google, commonly called "word2vec" (specifically, the "skip-gram" version of word2vec), widely used for learning representations of word relationships in written languages. The neural net is so simple it's not even properly a deep neural net.

A word2vec model consists of just two transformations. The first one takes as input a word and transforms it into a different representation. The second one transforms that representation into a prediction of the words surrounding the input word in a sample text -- say, the three preceding and succeeding words. As always, both transformations are mathematical, but you don't need to understand the math to grasp conceptually how this model works. (If you are curious about the math and you have at least some prior exposure to vectors, matrices, multivariate calculus, and statistical inference, see this step-by-step explanation.)

We train this word2vec neural net with a large number of examples -- say, every sequence of seven words found in the English Wikipedia. In training, the neural net learns to predict which words are likely to surround each input word, with a probability for each possible surrounding word. In order to predict these probabilities, the neural net learns to transform words into representations that encode the patterns of organization of those words in relation to every other word. Words that have similar meaning, such as, say, "tasty" and "savory," tend to be surrounded by similar patterns of words, so they are transformed into similar representations.

Once the neural net is trained, we discard the predictive operation. We are left with a model that transforms any word into a small number of values that represent how the word relates to every other word in the language.

Example #2: Learning Representations of Objects in Images by Predicting Reconstructions

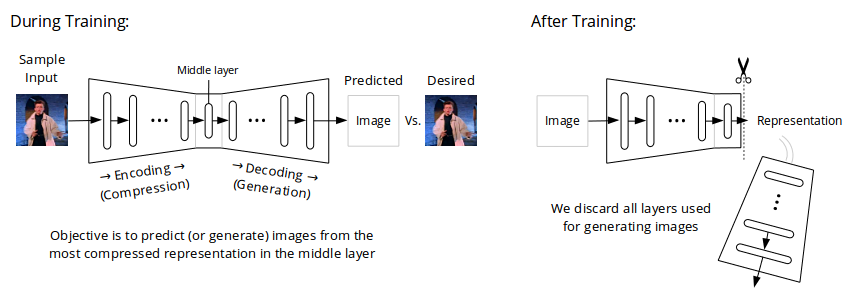
Our second example is a family of neural net models commonly called "stacked autoencoders" or simply "autoencoders," typically used for learning highly compressed representations of images. Unlike word2vec, autoencoders are currently not widely used in commercial applications; however, their design is intuitive and therefore relatively easy to explain, making them a suitable choice for use as an example here. There are many different autoencoder designs in the academic literature; two that have influenced our thinking at GlassRoom, for example, are "Denoising Autoencoders" and "Variational Autoencoders."

Autoencoders consist of two sequences of layers, with a layer sandwiched in the middle, between the two sequences. The first sequence has layers of decreasing size that take as input a large number (potentially millions) of pixel values making up an image and progressively transform them into a small representation in the middle layer (say, a few thousand values). The second sequence has layers of increasing size that progressively transform the small representation in the middle into a prediction of all pixel values that make up the input image -- i.e., a reconstruction or regeneration, if you will, of the input image.

When we train an autoencoder with a large number of examples (say, a few million digital photos), it learns to compress input images into small representations in the middle layer that encode patterns of organization of the portrayed objects necessary for regenerating close approximations of those images.

After training, we discard all layers following the middle one. We are left with a neural net that transforms images with millions of pixels into a small number of values that represent the objects in those images.

Example #3: Learning Representations of Meaning by Predicting Other Representations

Our final example is a family of neural net models commonly called "sequence-to-sequence" or "seq2seq" for short. Two prominent seq2seq models that have influenced our thinking at GlassRoom are Google’s Neural Machine Translation System and Facebook's Convolutional Sequence-to-Sequence Architecture. A seq2seq model takes as input a sequence of variable length, such as, say, a sequence of words with meaning in English, and learns to transform it into predictions of another sequence, such as a sequence of words in French with the same meaning -- i.e., a translation.

When we train a seq2seq model with many samples (say, many millions of sentences in English with the corresponding translations in French), it learns to transform sentences in English into representations of the patterns of organization of English words necessary for generating French translations. Put another way, the neural net learns to transform patterns of thought, or meanings, from one representation (written English) to another (written French); in order to do that, the neural net learns representations of those meanings.

After training, we discard the layers used for generating French translations. We are left with a neural net that transforms sentences in written English into values that represent their meaning.

We Use Proven Design Patterns for Novel Representation Learning Tasks

You might be thinking, how does anyone come up with these designs? Do we start from scratch?

The answer to the first question -- how does anyone come up with these designs? -- depends on the problem at hand. At GlassRoom, to the extent possible, we use existing, proven deep learning architectures as starting points. Nonetheless, our experience is that for novel representation learning tasks, engineering generally becomes an iterative process requiring a bit of thinking and then some experimentation, followed by a bit more thinking and then some more experimentation. We are guided more by domain-specific insight than by theoretical first principles, like builders of bridges before Newton's discovery of the laws of Gravity. The work is never really "finished." Indeed, we expect to be thinking up and testing potential improvements to our deep representation learning models indefinitely -- or at least until breakthroughs in AI make it unnecessary.

The answer to the second question is no: we don't start from scratch. Instead, we tend to use and reuse a set of proven design patterns -- think of them as recipes -- that can be combined in different ways to build neural nets for a broad range of representation learning tasks. In fact, in the three examples we examined above, you can discern three design patterns: the skip-gram version of word2vec learns representations of word relationships by predicting context; autoencoders learn representations of objects in images by predicting reconstructions; and seq2seq models learn representations of meaning by predicting other representations. At GlassRoom, we use these and other design patterns to construct representation learning models.

Why and When is Deep Representation Learning Necessary?

In our experience, there are three very compelling reasons to use deep representation learning:

1. If you don't have enough training data.

2. If you have zero examples for many categories of the objects of interest.

3. If your problem requires a model more computationally complex than feasible.

In all cases, we assume the problem at hand is complicated enough to require deep learning.

Reason #1: You Don't Have Enough Training Data

Let's say you need to build and train a machine learning model for classifying written customer reviews as having positive or negative sentiment -- a fairly common machine learning task. Now, imagine your sample data consists of only, say, a dozen thousand reviews, each labeled as positive or negative -- which is not a lot of labeled data. No matter what kind of model you train with those labeled reviews, the model will only be able to learn from the patterns present in your small data set, and might do poorly when faced with new data.

In other words, there isn't enough training data. This is probably the most common problem in machine learning.

One way to overcome this problem is by exploiting representational knowledge learned from another dataset of reviews which are not labeled as positive or negative. We would first train a model to learn representations of the unlabeled reviews. Then, we would then use the trained model to transform labeled reviews into representations of user review patterns, and feed those representations as inputs to train a classification model, which would benefit from the representational knowledge learned from the unlabeled reviews:

A team of researchers at OpenAI did that in 2017. They trained a model to predict the next character from previous characters on each of 82 million unlabeled Amazon reviews, and then used the representations learned by this character-level model as inputs to a simple sentiment classification model, which produced then-state-of-the-art results in a range of datasets used in sentiment-classification research.

The term of art for this feat is transfer learning, so called because we transfer the representational knowledge learned in one task (prediction of next character in unlabeled reviews) to another task (prediction of sentiment).

Reason #2: You Have Zero Examples for Many Categories

"Suddenly, a Leopard Print Sofa Appears" is the title of a blog post about deep neural nets that went viral with AI researchers, software developers, and technologists in 2015. The author of the blog post had downloaded a deep neural net pretrained to classify images into 1000 categories, including category number 290, representing "jaguar or panther, Panthera onca, Felis onca." He then fed the image below to the pretrained neural net, which naturally predicted category 290 as the most probable among the 1000 seen in training:

Why would anyone expect more from a deep neural net trained to predict probabilities among only 1000 possible different categories? A deep neural net trained to predict probabilities among 1000 categories cannot predict a category outside the range of 1 to 1000, by design. If we feed a photo of an object not belonging to any of those categories, the neural net will dutifully make nonsensical predictions between 1 and 1000.

In other words, many categories are absent from the training data, so the neural net cannot learn to predict them. This too is a common problem in machine learning, typically manifested as poor predictions for unexpected input data -- e.g., a silly prediction like "jaguar or panther" for a leopard-print sofa.

One way to sidestep this problem is by predicting better representations of the objects of interest instead of discrete categories such as 1 to 1000. In general, discrete categories are poor representations, because their only pattern of organization is that they are different from each other -- they provide no clue as to how or why they are different.

For example, we could first train a word2vec model, like the one described earlier, to learn representations of every word in English that encode how each word relates to every other word in the language. Then, we would train the neural net for image recognition to predict representations of the words which best describe each of the 1000 categories available in the training data:

Once trained, the neural net we are using for image recognition would predict, not discrete categories, but representations of relevant patterns of organization, each easily associated with a specific word. The predicted representations would encode how each input image relates to other images in terms of the words that best describe them. Were we to feed images of previously unseen categories to this neural net, it would predict representations that can be easily associated with words that describe those images.

In fact, a team of AI researchers at Google did exactly that in 2013, two years before the blog post about the leopard-print sofa. The Google researchers trained a deep neural net to predict corresponding-word representations with image samples from only 1000 categories. Once trained, the neural net was able to make sensible predictions for images from tens of thousands of other categories it had never seen before. Moreover, its prediction errors made more sense to human observers. For example, the predicted representation for an image of an English horn, which the neural net had never seen before, was more closely associated with the word "oboe." To most human beings, the two musical instruments look almost exactly alike.

The term of art for this otherwise seemingly impossible feat is zero-shot learning, so called because the neural net learns to recognize objects after seeing them exactly zero times.

Reason #3: Your Problem Requires a Model More Complex than Feasible

As the tasks we attempt with AI become more difficult, the objects of interest tend to become rarer, because their structure gets more complicated -- i.e., they have more interconnecting parts, and therefore are less common than those parts. For example, in English literature there are fewer paragraphs than sentences, fewer book chapters than paragraphs, and fewer books than book chapters. Similarly, in a video game like Minecraft, which allows players to construct objects from virtual blocks, there are many fewer million-block structures than thousand-block structures. Consequently, the maximum possible number of samples available for training a model tends to decline as the learning task becomes more difficult and the objects of interest become more complicated.

At the same time, the more complicated the structure of the objects of interest, the greater the number of computational steps required to discern their patterns of organization. For example, to learn to discern objects in complicated scenes depicted with millions of pixels, we can't use a tiny, shallow neural net with, say, a few thousand neurons; we need deep neural nets with many millions of neurons. In general, objects of interest that have a more complicated structure require models of greater computational complexity.

A mathematical framework called PAC Learning Theory relates the probability that a machine learning model can approximately learn to recognize objects of interest to the model's computational complexity and the number of training samples. The theory's details lie well beyond the scope of this web page, but its practical implications, widely verified in practice, are highly relevant to the foregoing: models that are more computationally complex tend to require a greater number of training samples.

Thus, as we attempt more difficult AI tasks involving more complicated objects, we tend to have fewer samples, but we also must use models that perform more computations, which therefore require more samples. Do you see the problem?

We conjecture there is a frontier beyond which the complicated structure of the objects of interest requires models more computationally complex than is feasible given the declining maximum possible number of samples available. We don't know if this frontier's existence can be (or has already been) proved by a mathematician or theoretical computer scientist. We also don't know if this frontier is somehow an inherent limitation of current technology, such as the crude iterative method we use for training models like deep neural nets in end-to-end fashion (all layers jointly). What we know is that on the other side of this frontier, we need more "powerful" models, as it were, to discern more complicated patterns of organization, but if we make our models more powerful, we need more samples than we can possibly have, so we cannot make our models more powerful.

At GlassRoom, we are familiar with the contours of this frontier, if you will, because our objects of interest, public companies, are complicated entities made up of only slightly less complicated parts arranged in complicated ways, described only in complicated book-length documents that presume the reader has extensive prior knowledge of industries, businesses, finance, and accounting.

For a typical example, consider The Coca-Cola Company. Its 2017 annual report contains 164 pages of explanations, excluding attachments, carefully edited by an army of executives, accountants, and lawyers to meet disclosure requirements. (If, like most people, you have never seen an annual report before, we suggest you browse this one from beginning to end so you can appreciate how much information it contains.) Besides the annual report, there are many other important sources of relevant data for Coca-Cola, including interim reports issued by the company itself, information issued by competitors, and economic data collected and released by a range of government agencies.

Human beings who analyze companies for a living find it challenging to learn to make sense of all this data. In the words of an acquaintance who runs an investment management firm employing highly-paid human analysts:

"We hire the best young people we can find, educated at the finest educational institutions in the world, and for many years they do what they're told, going through the motions of reading company reports, interviewing management teams, building spreadsheet models, and writing internal investment memorandums without really understanding what they're doing. It's only after about a decade that things finally click for them and they start recognizing high-level patterns and develop an intuition for reasoning about different businesses."

The number of samples is small. As we write this, the total number of annual reports in US history available in electronic format from the Securities and Exchange Commission is only around 200,000. Note that this is the number of annual report samples; the number of distinct companies is an order of magnitude smaller, because most companies file more than one annual report during their existence. Even if the number of annual reports were an order of magnitude greater, it would still pale in comparison to the complicated structure of each point-in-time sample, making it infeasible, we believe, to build end-to-end machine learning models with the computational complexity necessary to discern patterns as well as a competent human analyst.

To the best of our knowledge, there is no known solution to this obstacle. So, how do we surmount it?  Our workaround will seem obvious in hindsight: we break up the objects of interest into simpler component objects, each of which requires a less computationally complex model. That is, we use simpler models to learn representations of simpler "parts" or "aspects" of each company, obtaining multiple component representations per company. Then, we use these component representations, which have discarded a lot of information, as inputs to another model, also simpler than otherwise necessary, for learning representations of entire companies. In short, we break up what otherwise seems to be an intractable problem into tractable representation learning subproblems.

Figuring out how to break up the objects of interest into simpler components is non-trivial, requiring both domain expertise and engineering effort. However, barring new, fundamental breakthroughs in the way AI models are built and trained, we don't know of a better workaround.

For lack of a better term, we call this approach component learning.

Final Thoughts

We hope you now understand what deep representation learning is, why and when it is necessary, and how we use it at GlassRoom to make sense of our objects of interest: public companies. We also hope your mind is now brimming with ideas for applying transfer learning, zero-shot learning, and component learning to real-world problems -- ideas that might have seemed almost science-fiction before you started reading this web page.